Pares de Rectas

Rectas paralelas y perpendiculares

Nuestro objetivo es graficar los 4 puntos para servir de apoyo y obtener los ángulos formados entre estas 2 rectas, y mediante las características de las rectas paralelas o perpendiculares identificar cual de estas son, para que no solamente usar la geometria analitica, sino que tambien, aprender a usarlo en conjunto con las TIC’s.aprender a relacionar circunstancias de la vida cotidiana con la geometria analitica o mas bien con la matematica en general.

Conceptos e ideas que se tomarán en cuenta

Pendiente:
La pendiente es la inclinación de la recta con respecto al eje de abscisas, se denota con la letra m.
La pendiente de una recta es la tangente del ángulo que forma la recta con la dirección positiva del eje de abscisas.

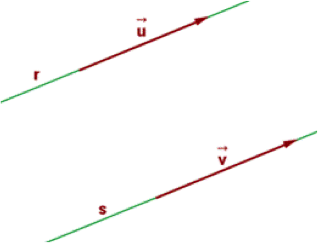
RECTAS PARALELAS

Se denominan rectas paralelas las líneas que mantienen una equidistancia entre sí, y que, aunque prolonguemos su trayectoria hasta el infinito, nunca, en ningún punto sus trazos pueden bifurcarse, tocarse, encontrarse. Es decir, entre ambas líneas (aunque pueden ser planos lineales de mayor dimensión, como ya veremos) se establece una relación de paralelismo.

Dos rectas paralelas y su pendiente (m)

Dos rectas son paralelas si tienen sus pendientes iguales.
 Formula Pendiente: M1= M2

La  pendiente encontrada en una ecuación seria la misma para el otro punto dado. Y luego se usara la formula para sacar la ecuación de la recta.
M=y-y1/x-x1

Rectas Perpendiculares

1.   Dos rectas que se encuentran en el mismo plano son perpendiculares cuando forman cuatro ángulos rectos. En el caso de las semirrectas, la perpendicularidad aparece cuando se desarrollan ángulos rectos, por lo general con idéntico punto de origen.

2.   Los planos y semiplanos, por último, son perpendiculares en los casos en que se forman cuatro ángulos diedros de noventa grados

Rectas perpendiculares y su pendiente (m)

•Si dos rectas son perpendiculares tienen sus pendientes inversas y cambiadas de signo.

M1=-1/m2

•La pendiente encontrada en una ecuación, tendría que hacerse la formula ya vista y la pendiente dada seria perpendicular a la otra ecuación

M1=-1/m2 →  m=y-y1/x-x1

Formula pendiente m1*m2=-1

PENDIENTE E INCLINACIÓN DE LA RECTA

•Se denomina ángulo de inclinación de una recta al ángulo que determina dicha recta con el sentido positivo del eje x, siendo medido este ángulo en sentido contrario a las manecillas del reloj, desde el eje positivo de las x hasta la recta. El ángulo de inclinación de una recta es un valor que siempre esta comprendido entre 0 y 180°, además indica su posición en el plano:

•Así si una recta es paralela al eje x su Ð de inclinación es  de 0°.

•Si es perpendicular al eje x, su ángulo es de 90°.

•Si se inclina hacia la derecha el ángulo es agudo.

•Si se inclina hacia la izquierda su ángulo es obtuso

RECTAS OBLICUAS

Es aquella que, al intersecar otra recta, crea un ángulo que no mide 90º. Los ángulos creados por las rectas oblicuas, por otra parte, no son iguales (no miden lo mismo).

Dos rectas son oblicuas si sus pendientes no presentan los casos anteriores. 

Objetivos

•      Aprender a implementar la geometría en las TIC’S.

•      Relacionar sucesos de la vida Real con la geometria analitica o más bien las matemáticas en general.

•      Influenciar a las personas con actividades que retroalimentan la mente.

•      Compartir nuestra experiencia con otras personas a través de medios de comunicación como un ejemplo:el internet.

Este proyecto lo estamos haciendo para reforzar nuestros conocimientos aprendidos a lo largo del semestre y para que este mismo proyecto, pueda ser revisado y sirva como guia o base para ayudar a otras personas para que elaboren proyectos del mismo nivel que este o incluso mas grandes que este, todo esto hecho mediante el internet que sirve como medio de comunicacion que conecta a las personas en una red masiva.

Planteamiento del problema

Este proyecto de Geometría Analítica se realizó con el fin de usar las TIC’s como recurso para resolver problemas de nivel medio superior, ya que al grado de aprendizaje en el que estamos es indispensable utilizar herramientas como Excel (por ejemplo) para elaborar proyectos o sencillamente comprobar resultados obtenidos en los ejercicios del libro o del facilitador.

   Problema

Elaboren una hoja de cálculo en la que dados 4 puntos. Calculen el ángulo que  se forma entre las 2 rectas. Incluir condiciones  si son perpendiculares, paralelas.

Como observamos en la siguiente imagen es el problema ya realizado por el  equipo numero 9

 el cual esta conformado por:

Edgar Alvarez Zapien.

Carlos Adalberto Ayala Argumedo.

Samuel Yobany Ayala Salmeron.

Jesus Corvera Contreras.